Introduction, example, and algorithm draft
If a word or a company name is misspelled, how to measure the distance with its reference?
For instance, how to build one mathematic model, amongst many others, determining that Goggle is closer to Google than to Amazon, Facebook, or Apple?
The Levenshtein distance will be treated with 3 posts:
- Introduction of the Levenshtein distance definition, an example called « GAFA », and starting to explain the classical algorithm required for calculating the distance [this post]
- The full algorithm and the full definition of the Levenshtein distance
- Using R programming for solving the « GAFA » example with Levenshtein distance
A short definition of the Levenshtein distance
The Levenshtein distance measure the distance, as a metric, between two sequences (words, character strings…).
The result is provided as a whole number.
Indeed, the distance is the minimum number of single-characters edits, for going from one sequence to the other sequence, through 3 tools:
- Inserting a character
- Deleting a character
- Substituting a character
A very simple example: the distance between car and cat is 1, as you only need to substitute the last letter of car, from r to t, in order to retrieve cat
The GAFA example
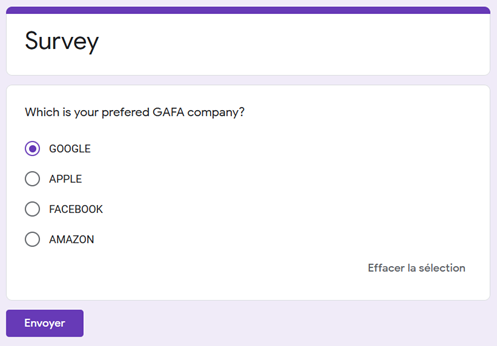
Consider we have received a Google Form survey result, where people were asked to enter their favorite GAFA, meaning choosing between Google, Apple, Facebook, and Amazon.
In an ideal scenario, a drop-down list is created, hereunder a survey creation example with a Google Form.
With this ideal form, no mistake is possible for the user:
But if no validation has been set up (due to mistake or because this functionality is unknow) in the form configuration, and if the answer is a free short text.
Then, misspelling is possible.
The failed-soft form proposed to the user:
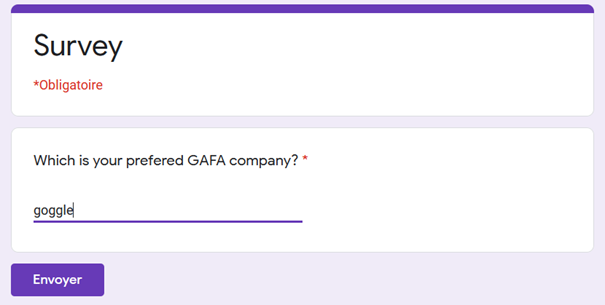
Some examples of misspelling :
- Gogglle
- Gougeule
- Googe
- Amazon
- Amzone
- Firstbok
- Alpes
- Aple
Remark: for this entire post, we won’t consider case-sensitive:
‘A’ is considered the same as ‘a’, ‘B’ is considered the same as ‘b’…
The question: after the result of the survey has been received, how to guess the relevant answer in case of misspelling?
| Answer in the survey… | … was probably meaning |
| Gogglle | |
| Gougeule | |
| Googe | |
| Amazon | Amazon |
| Amzone | Amazon |
| Firstbok | |
| Alpes | Apple |
| Aple | Apple |
An intuitive application of the Levenshtein distance
Is the sequence » Gogglle » closer than the sequences « Google », « Apple », « Facebook », or « Apple »?
For a human, the answer is reasonably « Gogglle » is closer to « Google ». But how could a computer answer to that? It’s why we introduce the Levenshtein distance, which is one method amongst many.
Remember we have these hereunder 3 tools, and apply them:
- Inserting a single-character
- Deleting a single-character
- Substituting a single-character
| From Sequence | To Sequence | Succession of intuitive operations required | Intuitive operations total |
| gogglle | Substitute the third letter of gogglle: the result is googlle Delete the fifth letter of googlle: the result is google | 2 | |
| gogglle | apple | Delete the first letter of goggle: the result is ogglle Delete the first letter of ogglle: the result is gglle Substitute the first letter of gglle: the result is aglle Substitute the second letter of aglle: the result is aplle Substitute the first third of aplle: the result is apple | 5 |
| gogglle | You can now apply an intuitive method on your own… | ||
| gogglle | amazon | You can now apply an intuitive method on your own… |
We keep in mind:
- The intuitive method provides a metric, as a whole number
- The closer the distance, the less the metric
In this example, we note that the distance “gogglle-google” is 2 and lower than the distance “gogglle-apple” which is 5. We can reasonnably deduce that the surveyed person who has entered “gogglle” was meaning “google” and not “apple”.
From now, “gogglle-google” will be our own official notation for the distance between « gogglle » and « google »
With complex sequences, the intuitive application isn’t enough. There might be some mistake in the previous calculation. It’s why we need a realiable method.
Draft of a reliable algorithm calculating the Levenshtein distance
In order to follow a learning curve, we will grope during the assembling of this method.
Introducing the matrix shape into the method
Let’s take an example pointing out a pitfall in the intuitive distance calculation: what is the distance between “eval” and “valley”?
A very quick intuitive operation would be to apply:
| From | To | Succession of intuitive operations required | Intuitive operations total |
| eval | valley | Subsitution of first letter of eval: result is vval Subsitution of second letter of vval: result is vaal Subsitution of third letter of vaal: result is vall Insertion letter at the end of vall: result is valle Insertion letter at the end of valle: result is valley | 5 |
A more rigorous intuitive operation would be:
| From | To | Intuitive and rigorous operation | Intuitive operations total |
| eval | valley | Removing letter at the beginning of eval: the result is val Inserting letter at the end of val: the result is vall Insertingletter at the end of vall: the result is valle Inserting letter at the end of valle: the result is valley | 4 |
The trick is: the 3 tools shouldn’t be applied systematically by starting at both words. We have to compare every substring from the first word (beginning, between, end) to every substring to the second word(beginning, between, end), in order to find the right approach.
There are two consequences, with 4 impacts:
| Consequence | Impact of the consequence |
| The optimal distance can use subtrings anywhere (beginning, starting at second index, starting at third…) in the first word, and anywhere (beginning, starting at second index, starting at third…) in the second word: all these combinations must be check | We will use a matrix shape: the abciss will reflect the first word, and the ordinate the second word |
| It is possible to break down the problem by removing the last character of the first sequence and removing the last character of the last sequence, and then treating the impact of adding one characters for each sequence | We will use recursivity: we will compare the distance between two words, with the distance of these two words without their last letter |
The matrix shape
A matrix will be applied as hereunder, for an example of finding the distance between “lalab” and “labo”. The global benefits are described hereunder
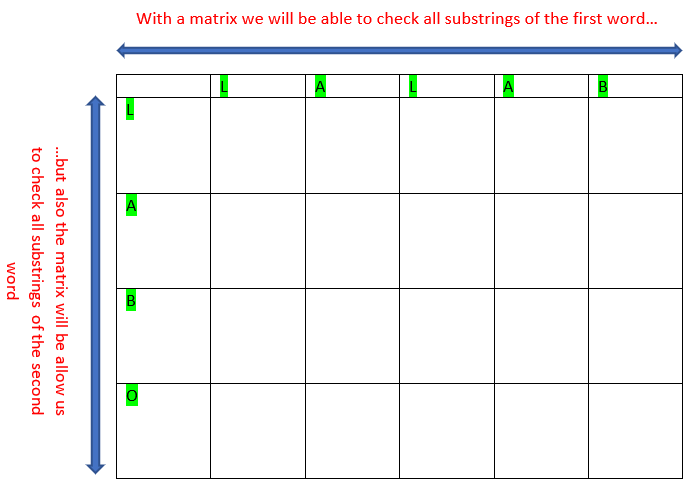
Intuitive application of the matrix shape
Remark: we start with an intuitive method, in order to get a progressive learning curve. You will state afterward, this is not very effective for the distance calculation. In the next post, we will learn to fill the matrix shape with the full-logic classical algorithm
Firstly, we decide to establish the distance between “lalalab” and « l », meaning to fill the first line. How to do it intuitively?
| L | A | L | A | B | |
| L | ? | ? | ? | ? | ? |
| A | |||||
| B | |||||
| O |
From L to L, the distance is 0, because no modification is required:
| L | A | L | A | B | |
| L | 0 | ? | ? | ? | ? |
| A | |||||
| B | |||||
| O |
From “L” to “LA”, the distance is 1, because after “L” you insert “A” and get “LA”:
| L | A | L | A | B | |
| L | 0 | 1 | ? | ? | ? |
| A | |||||
| B | |||||
| O |
From “L” to “LAL”, the distance is 2, because after “L” you insert “A” and “L”, and get “LAL”:
| L | A | L | A | B | |
| L | 0 | 1 | 2 | ? | ? |
| A | |||||
| B | |||||
| O |
From “L” to “LALA”, the distance is 3, because after “L” you insert “A” “L” and “A” and get “LALA”:
| L | A | L | A | B | |
| L | 0 | 1 | 2 | 3 | ? |
| A | |||||
| B | |||||
| O |
From “L” to “LALAB”, the distance is 24, because after “L” you insert “A” “L” “A” and “B” and get “LALAB”:
| L | A | L | A | B | |
| L | 0 | 1 | 2 | 3 | 4 |
| A | |||||
| B | |||||
| O |
Now, let’s fill the second line:
| L | A | L | A | B | |
| L | 0 | 1 | 2 | 3 | 4 |
| A | ? | ? | ? | ? | ? |
| B | |||||
| O |
From “L” to “LA”, the distance is 1, because from “L” you add “A”, and get “LA”:
| L | A | L | A | B | |
| L | 0 | 1 | 2 | 3 | 4 |
| A | 1 | ? | ? | ? | ? |
| B | |||||
| O |
From “LA” to “LA”, the distance is 0, because these are the same strings:
| L | A | L | A | B | |
| L | 0 | 1 | 2 | 3 | 4 |
| A | 1 | 0 | ? | ? | ? |
| B | |||||
| O |
From “LAL” to “LA”, the distance is 1, because from “LA” you add “L”, and get “LAL”:
| L | A | L | A | B | |
| L | 0 | 1 | 2 | 3 | 4 |
| A | 1 | 0 | 1 | ? | ? |
| B | |||||
| O |
From “LALA” to “LA”, the distance is 2, because from “LA” you add “L” “A”, and get “LALA”:
| L | A | L | A | B | |
| L | 0 | 1 | 2 | 3 | 4 |
| A | 1 | 0 | 1 | 2 | ? |
| B | |||||
| O |
From “LALAB” to “LA”, the distance is 3, because from “LA” you add “L” “A” “B”, and get “LALAB”:
| L | A | L | A | B | |
| L | 0 | 1 | 2 | 3 | 4 |
| A | 1 | 0 | 1 | 2 | 3 |
| B | |||||
| O |
Summary of the Levenshtein matrix
With the matrix, we can guess that we are covering every substring from the first word and every substring from the second word. Unhappily, the intuitive method will become inaccurate for the calculation of the difference. As a sample, “LABO” vs. “LALAB”. How to improve this algorithm draft?
The recursivity properties
Recursivity with same last letters
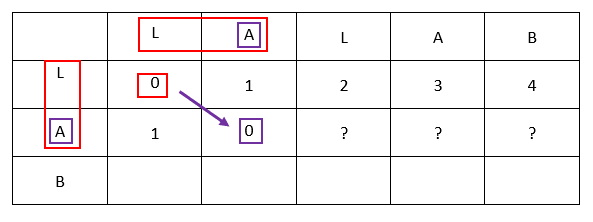
Let’s focus at this example:
| L | A | L | A | B | |
| L | 0 | 1 | 2 | 3 | 4 |
| A | 1 | ? | ? | ? | ? |
| B | |||||
| O |
The focus plot:
The recap:
- For example, we focus on the distance « LA-LA »
- It is the distance « L-L » + « A-A »
- We note that “A” and « A » are the same letters, hence the distance « A-A » is equal to 0
- Hence the distance from the cell [line “LA”; row “LA”] comes the cell [line “L”; row “L”] which is its up-left cell
If the letters are the same, we fetch the value from the upper left cell, which is the distance of the substrings without this same letter at the end:
Sum property with different last letters
Let’s focus at this example:
| L | A | L | A | B | |
| L | 0 | 1 | 2 | 3 | 4 |
| A | 1 | 0 | 1 | 2 | ? |
| B |
You notice the last letters are different.
The focus plot:
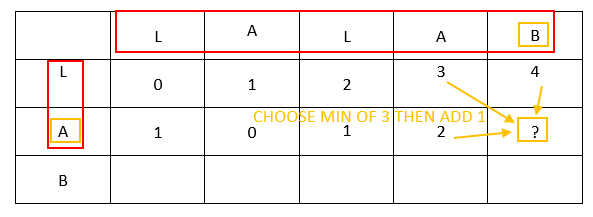
A recap:
- For the example “LALAB-LA”
- We have 3 candidates as the minimum distance:
- the distance « LALAB-L », plus the cost of « L » receiving at its end the insertion of « A« . Concretely the value of the cell [line “LALAB”; row “L”], which is the up cell, plus 1 which is the cost of insertion, is the first candidate for the “LALAB-LA” distance
- the distance « LALA-LA« , plus the cost of « LALA » receiving at its end the insertion of « B« . Concretely the value of the cell [line “LALA”; row “LA”], which is the left cell, plus 1 which is the cost of insertion, is the second candidate for the “LALAB-LA” distance
- the distance « LALA-L », plus the cost of subtituing « A » and « B« . Concretely the value of the cell [line “LALA”; row “L”], which is the up-left cell, plus 1 which is the cost of subtitution, is the first candidate for the “LALAB-LA” distance
Amonst these three candidates, how to choose the good one, with the minimum distance?
The distance, is by convention, and by practicality, the shortest path, hence the candidate with the lowest distance is the winner:

Conclusion of the Introduction, example, and algorithm draft
We have seen all the tools that will define the full algorithm of the Levenshtein calculation.
In the next post, we will fully detail and apply this algorithm.
In the last post, we will solve the GAFA example with R programming.
Application of the algorithm
Our example is to measure the Levenshtein distance between the word LABO and the company word LALAB, discovered in the previous post. They have been chosen, because it is difficult to intuitively guess their distance, due to common sub-strings.
Explanation of abscissa and ordinate:
LALAB is arbitrarily chosen as the abscissa word, as it will be written horizontally in the matrix
LABO is arbitrarily chosen as the ordinate word as it will be written vertically in the matrix
Remark: the Levenshtein distance is a commutative operation. It means the distance between LALAB and LABO is the same as the distance between LABO and LALAB. Hence, the abscissa and the ordinate could have been switched, and the result would have been the same.
Start of the classical algorithm example
Design a matrix with “LABO” as ordinate and “LALALAB” as abcissa:
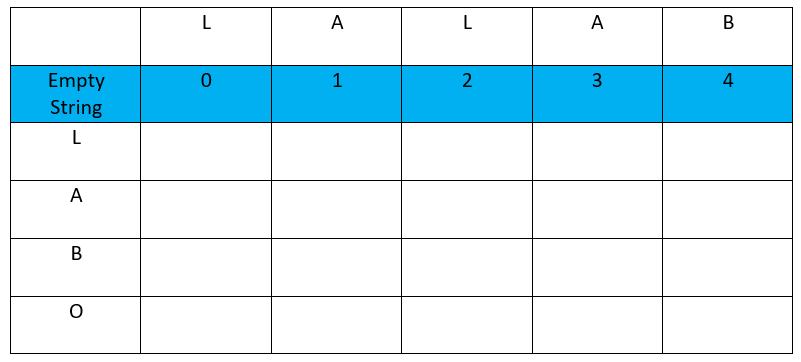
Add an initial row “empty string” and fill it with a numeric incremental sequence starting with 0 in front of the first offset of the abscissa word:
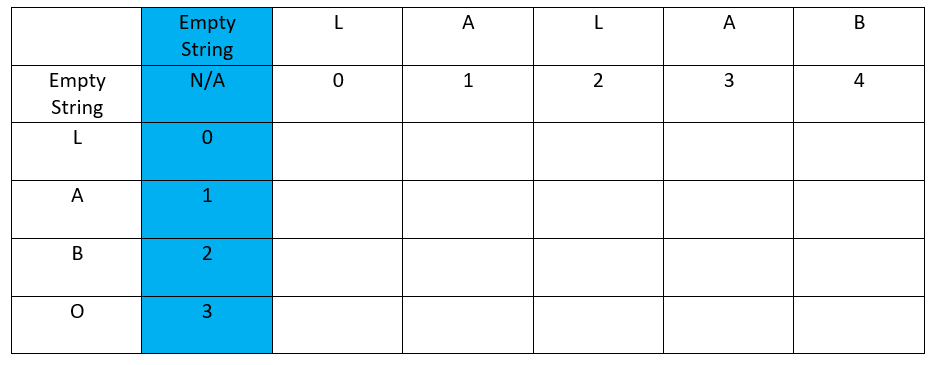
Add an initial column “empty string” and fill it with a numeric incremental sequence starting with 0 in front of the first offset of the ordinate word:
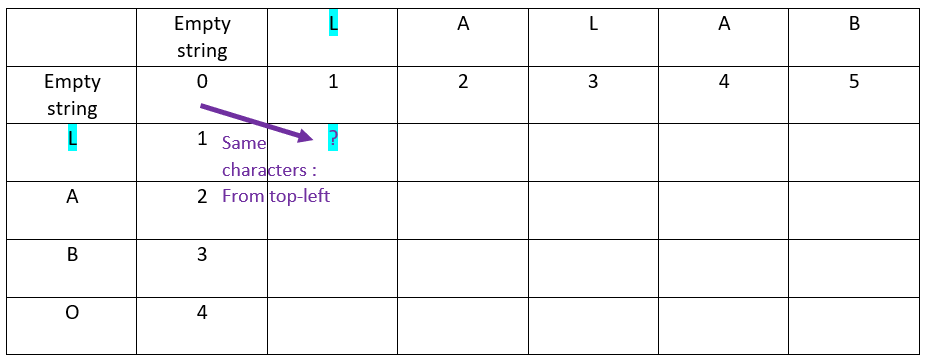
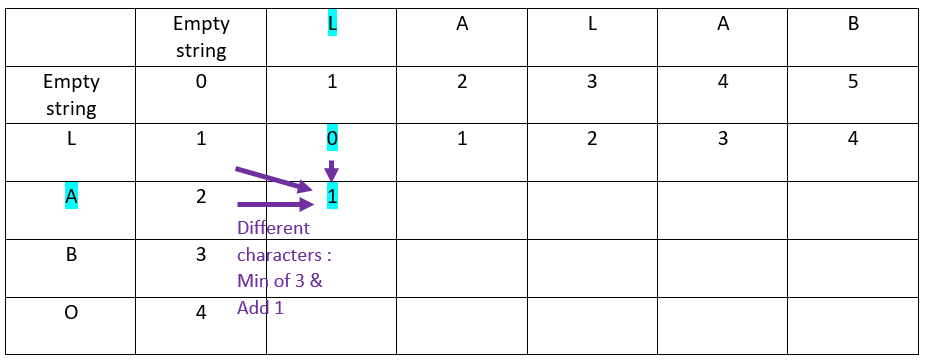
Let’s proceed with the first row, in front of the first offset of the ordinate word
Rule
When the characters in ordinate and in abscissa are the same:
The value is inherited from the top-left cell
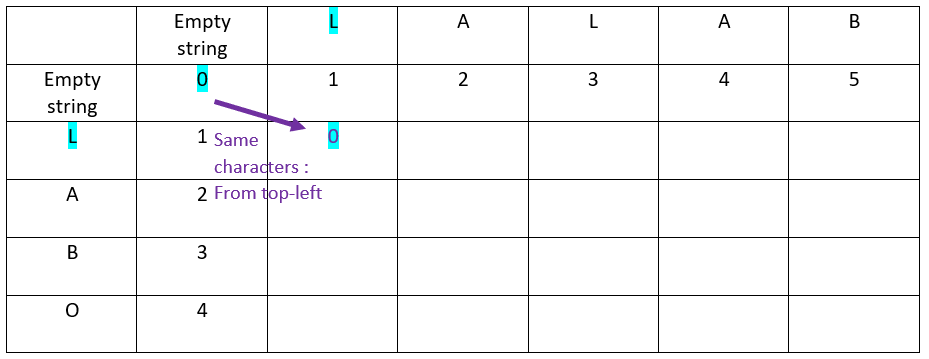
For the first cell, as the letters are the same, the ? value comes from the top-left cell:
The result is:
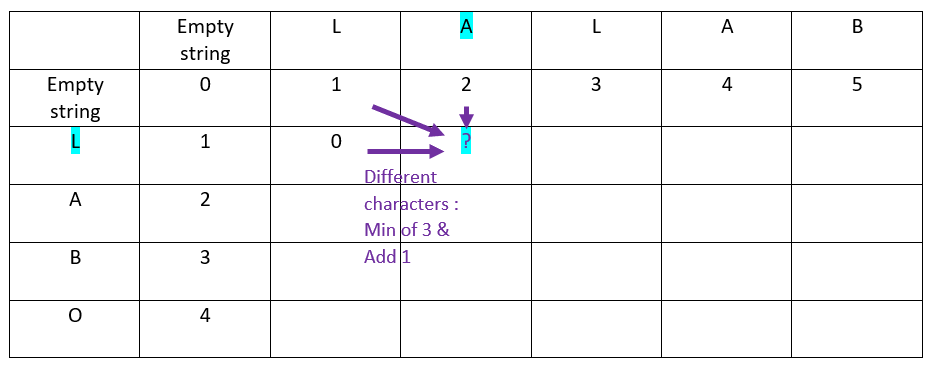
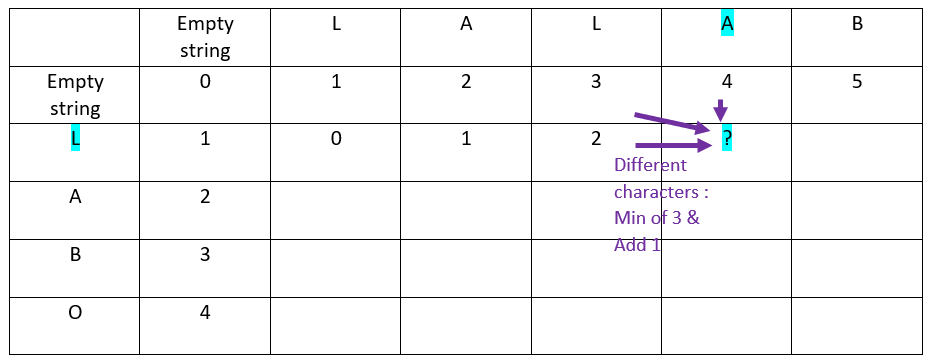
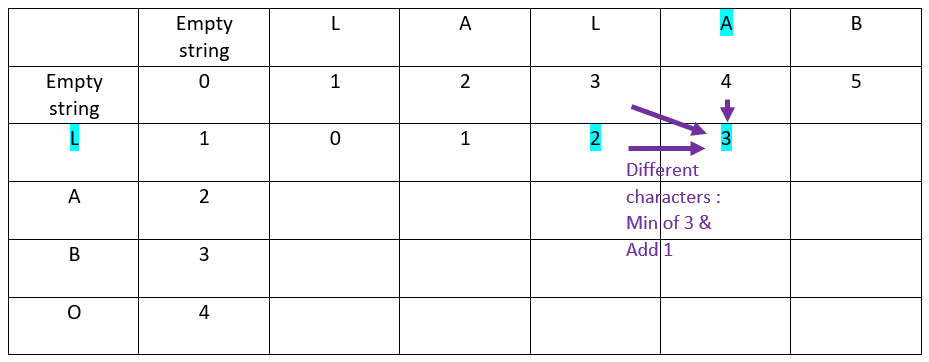
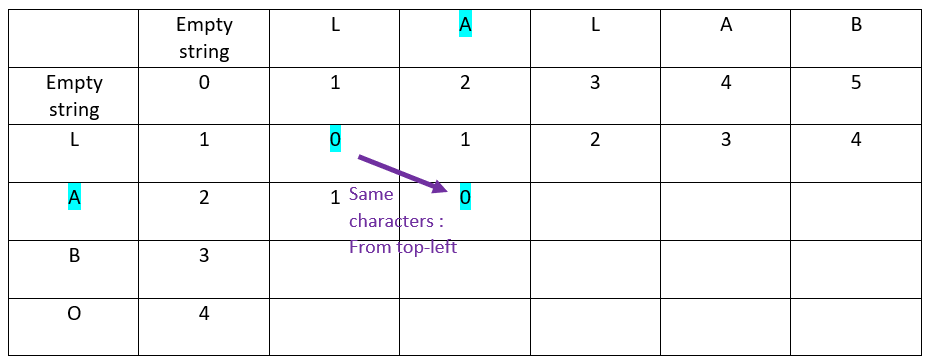
Rule
When the characters in ordinate and in abscissa are different:
The value is inherited from the minimum of:
– Top cell
– Top left cell
– Left cell
Then add 1 to the result
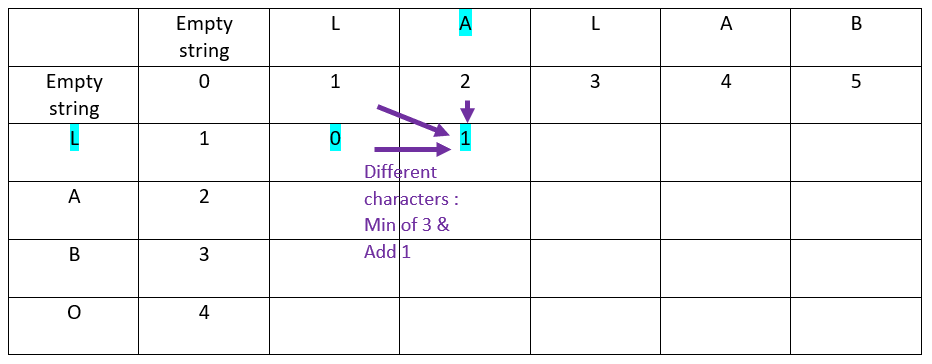
Now the second offset of the abscissa word:
The result is:
Now the third offset of the abscissa word:
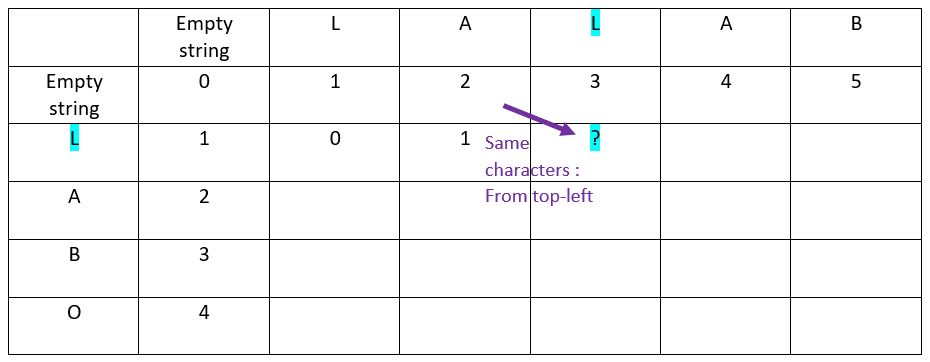
The result:
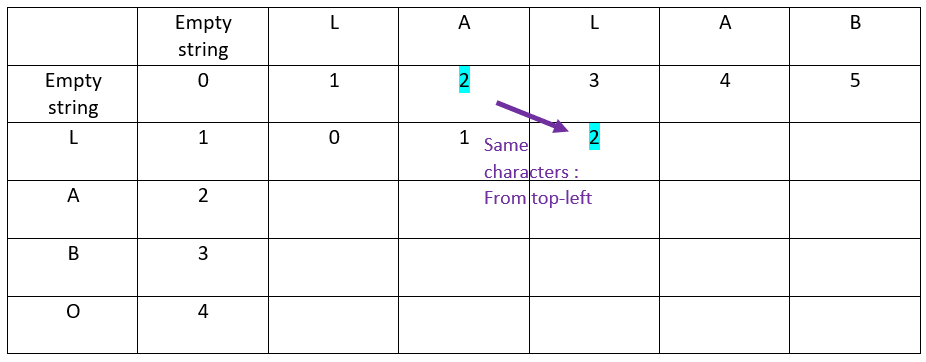
Now the fourth offset of the abscissa word:
The result:
Now the fifth offset of the abscissa word:
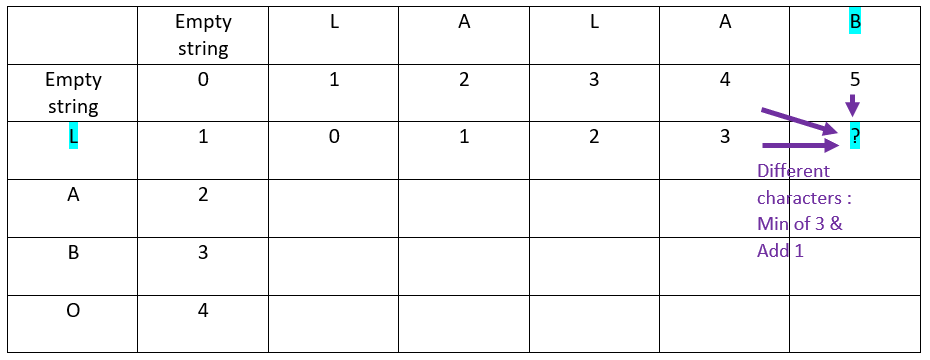
The result:
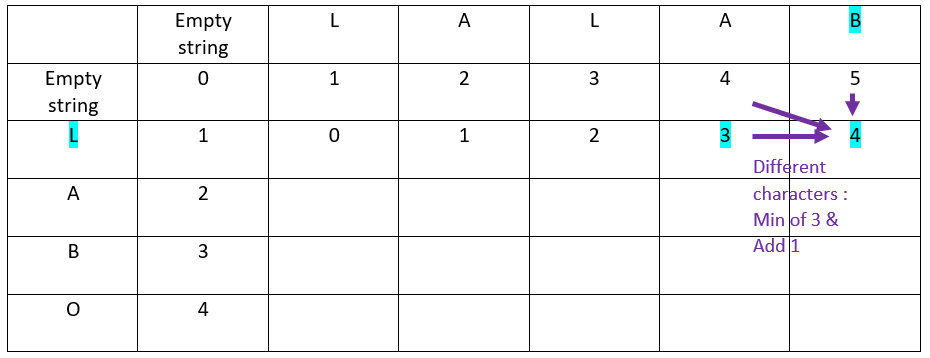
Let’s continue with the second row of the ordinate word:
First column:
Second column:
Third Column:
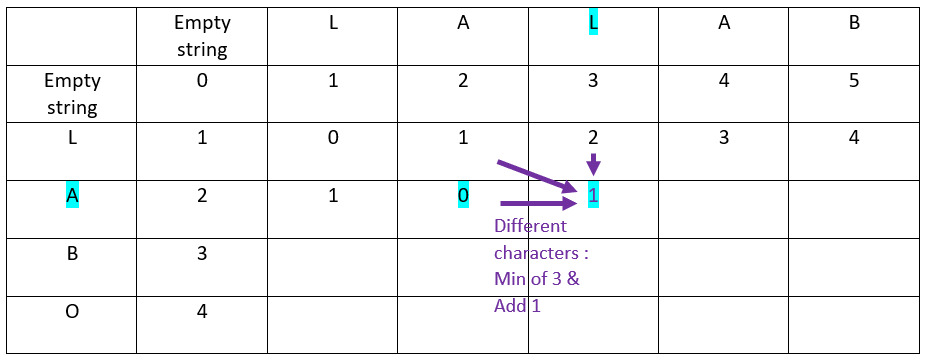
Fourth column:
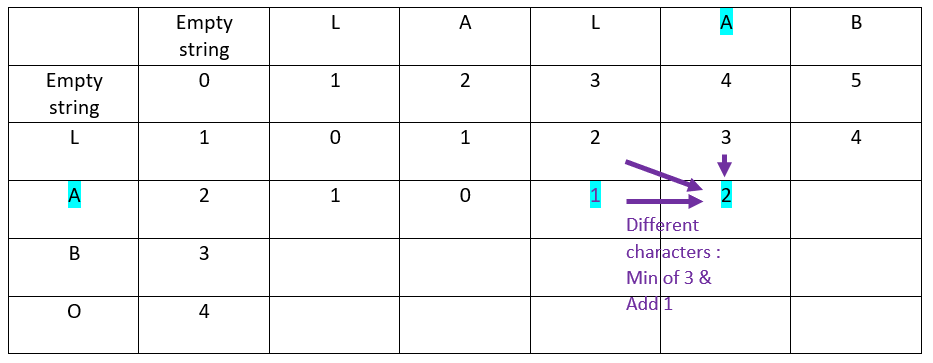
Fifth column:
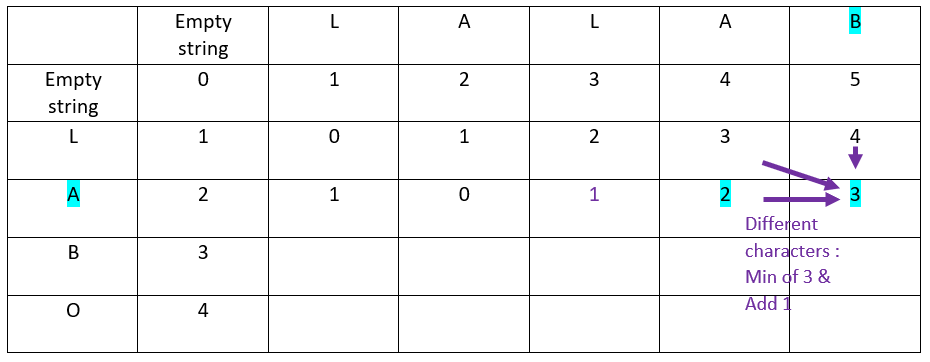
Let’s continue with the third row of the ordinate word:
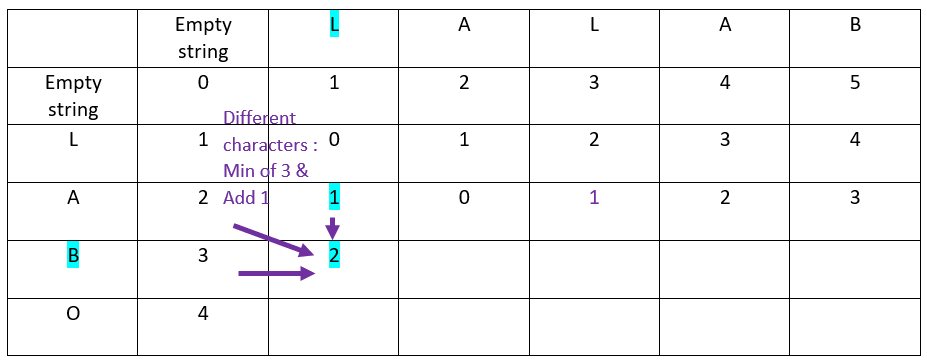
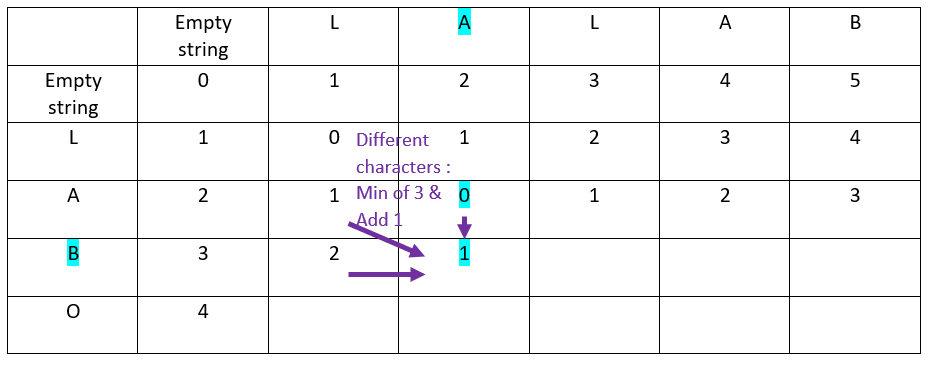
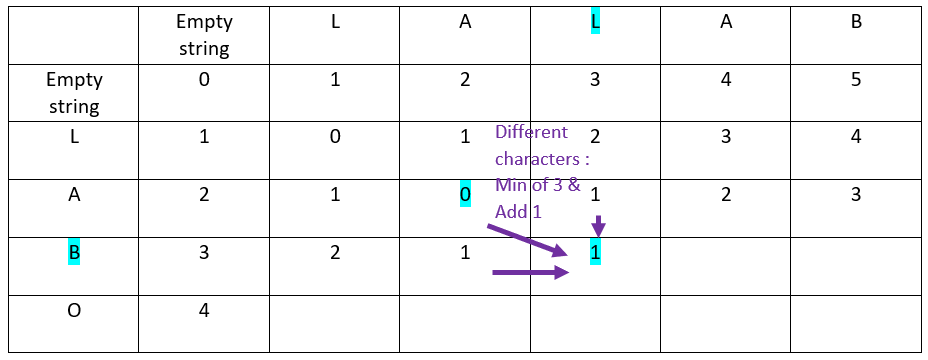
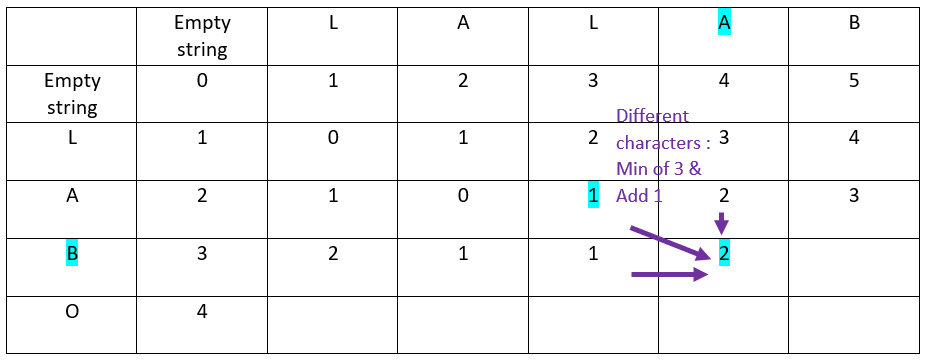
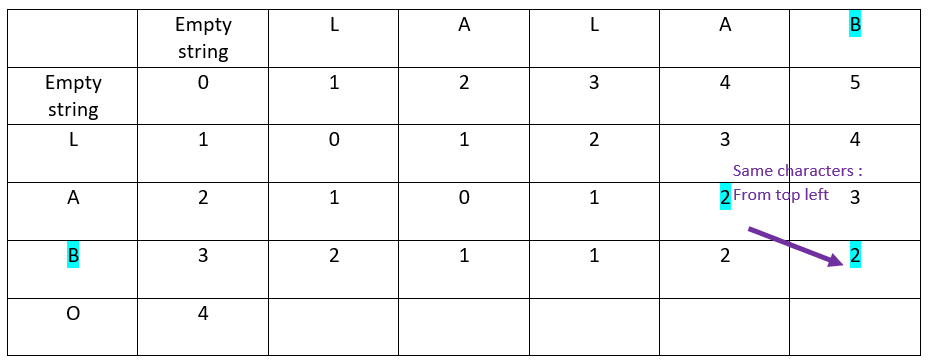
Let’s continue with the fourth and last row of the ordinate word:
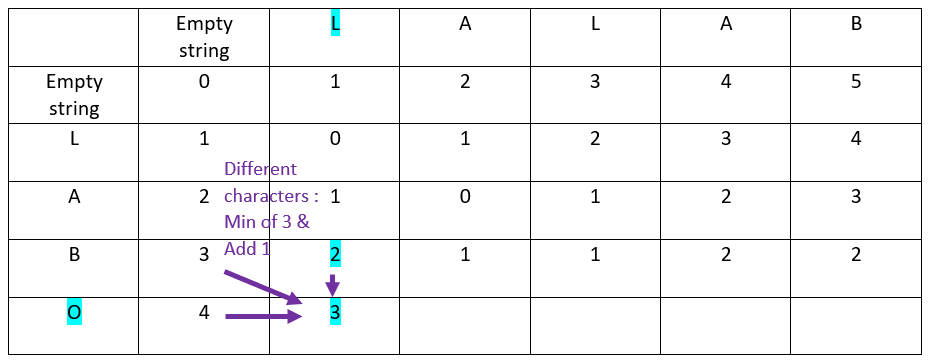
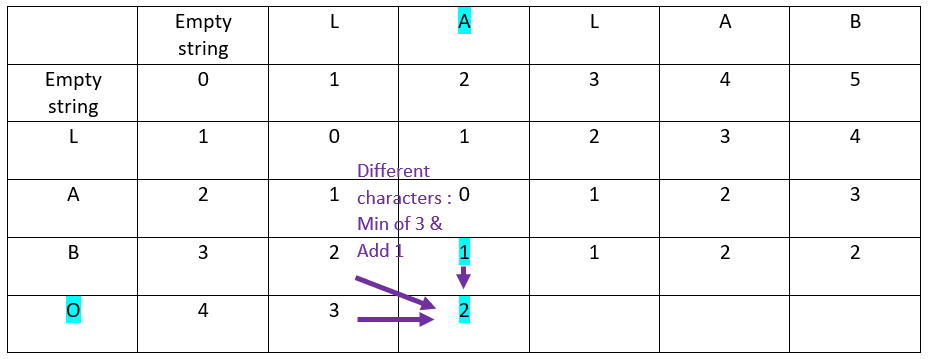
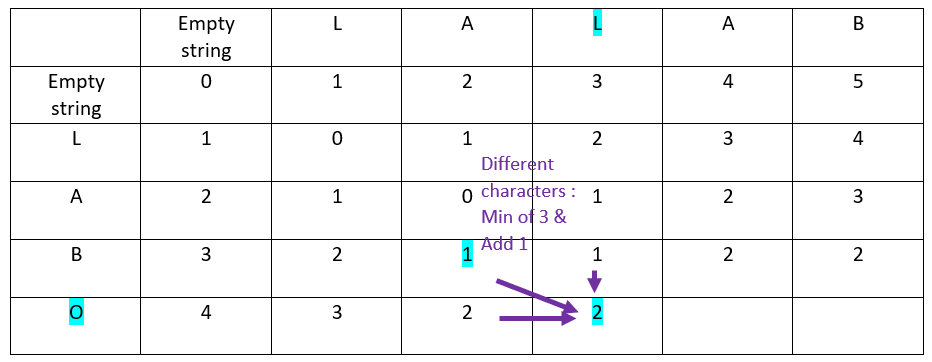
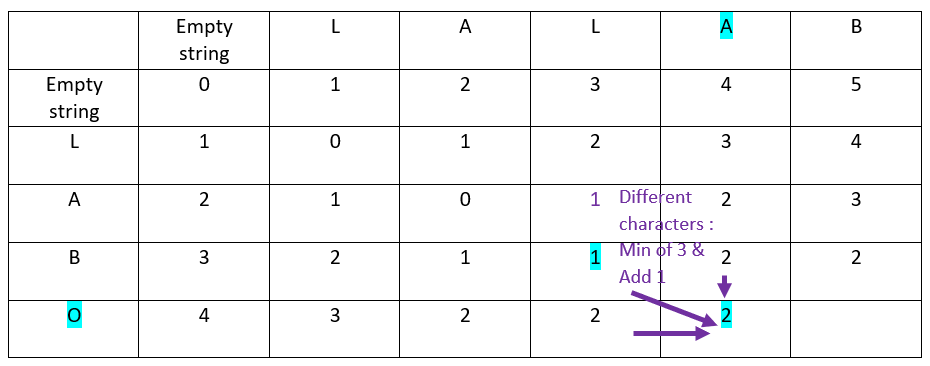
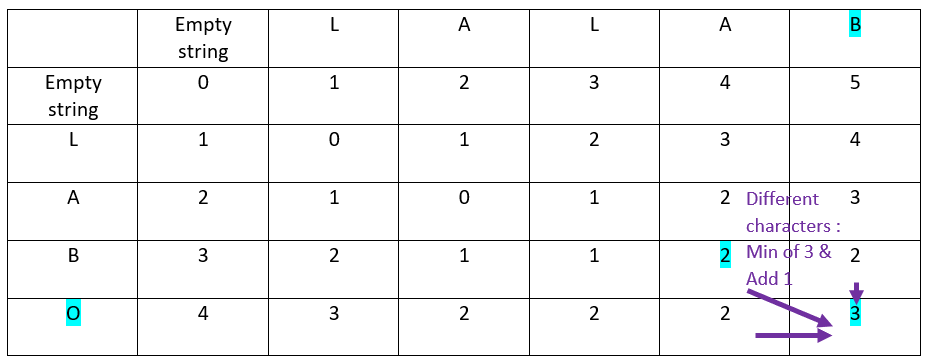
Analyzing the result of the applied algorithm
First information: what is the Levenshtein distance?
It is in the bottom-right cell: the distance is 3
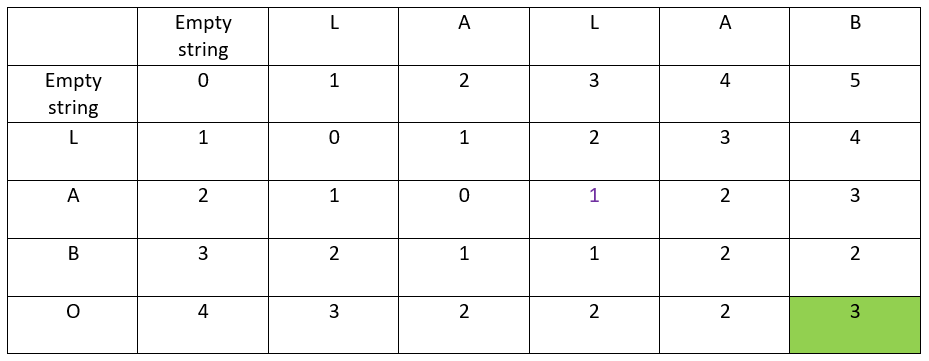
Second information: how to build the path leading from LABO to LALAB?
Summary of the applied algorithm
All possible solutions are found by building the path from the top-left cell to the bottom-right cell, cell by cell, with the following rules:
- each step must be going right, bottom, or diagonally bottom-right
- at each step, increase the distance, or at least keep it constant
- bottom-right diagonal has priority
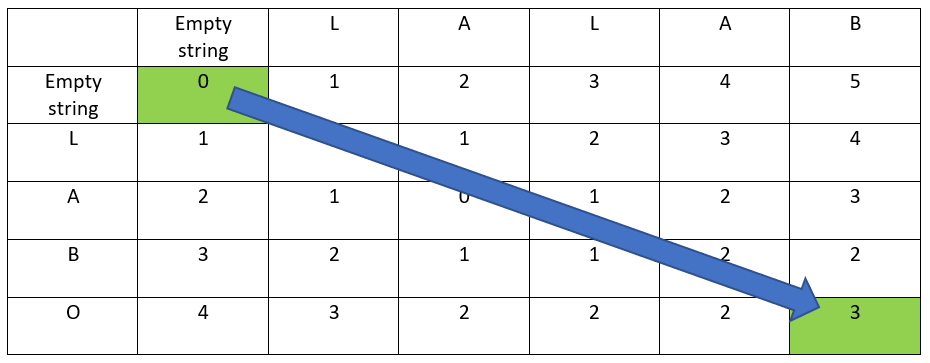
Hereunder one of the possible optimum paths:
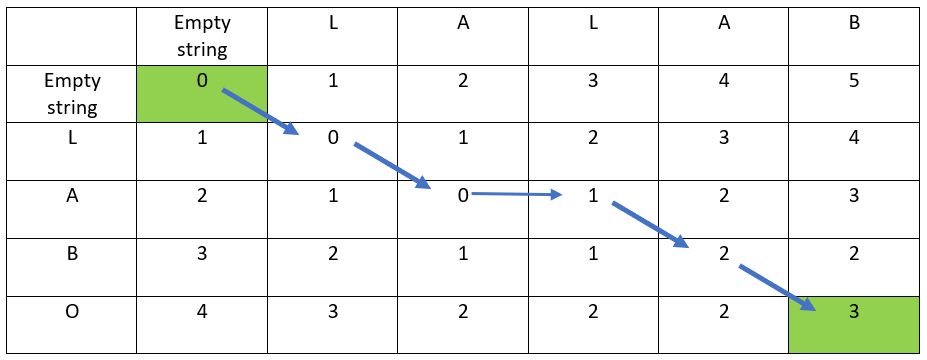
Application of the path to our example: explain how to go from LABO to LALAB
Reminder:
The three possibles tools with the Levenshtein distance are:
Insertion of character
Deletion of character
Substitution of character
Let’s start with the string LABO.
The hereunder red arrow indicates:
- the distance has not changed
- the ordinate & abscissa destination letters are the same
- hence the first letter is kept
- LABO has not changed: the result is still LABO
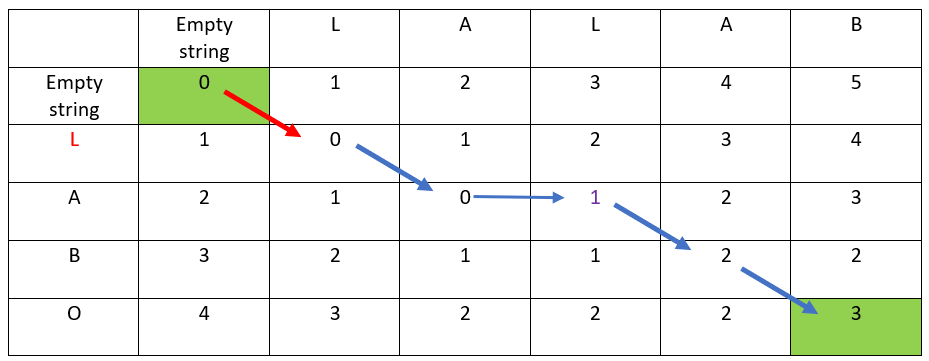
—
The hereunder red arrow indicates:
- the distance has not changed
- the ordinate & abscissa destination letters are the same
- hence the second letter is kept
- LABO has not changed: the result is still LABO
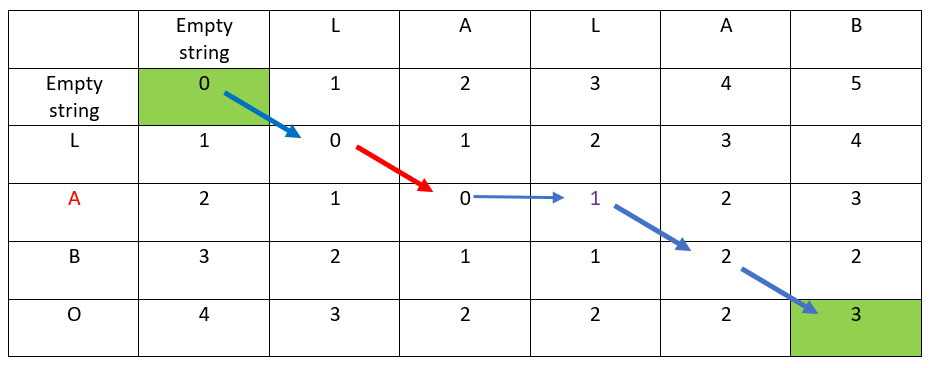
—
The hereunder red arrow indicates:
- the distance has increased: +1
- the ordinate & abscissa destination letters are different
- this is a « go right » arrow
- hence L has been inserted at the third offset
- LABO has changed to LALBO
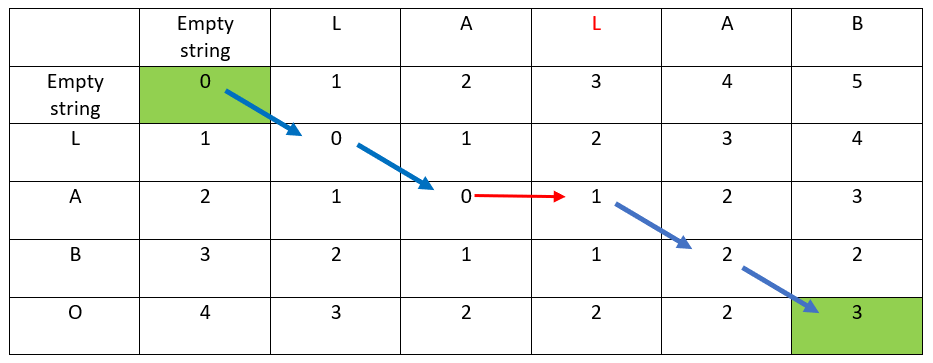
—
The hereunder red arrow indicates:
- the distance has increased: +1
- the ordinate & abscissa destination letters are different
- this is a « go down & right » arrow
- hence B has been replaced by A at the fourth offset
- LALBO has changed to LALAO
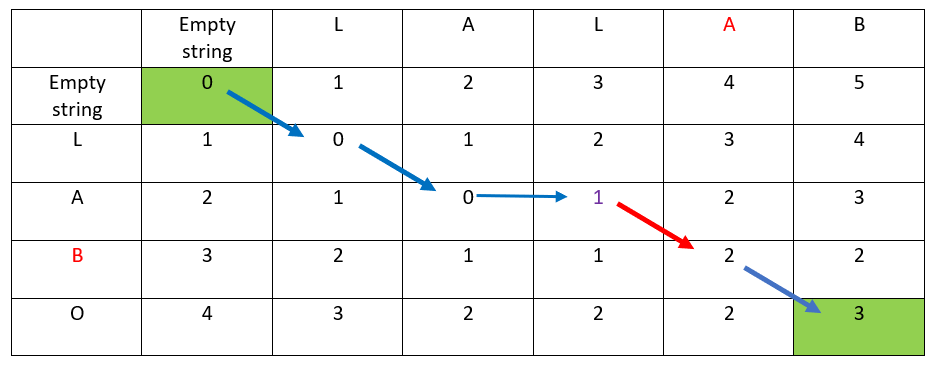
—
The hereunder red arrow indicates:
- the distance has increased: +1
- the ordinate & abscissa destination letters are different
- this is a « go down & right » arrow
- hence O has been replaced by B at the fourth offset
- LALAO has changed to LALAB
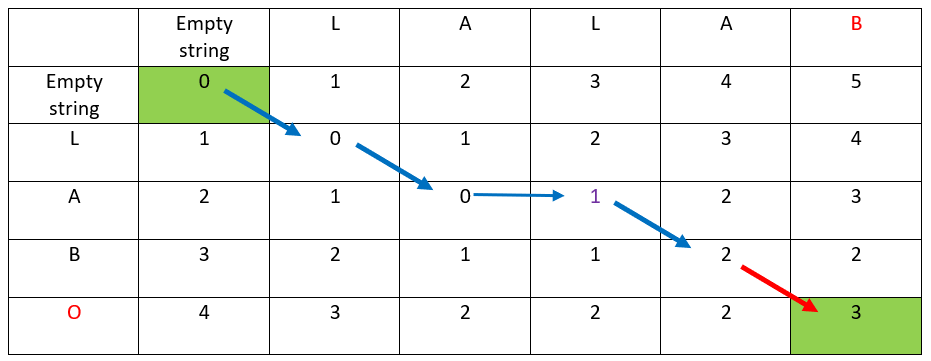
Rules for building the path
We just have studied the example. Now let’s describe it in generic terms.
First, we note there are three possible « steps »:
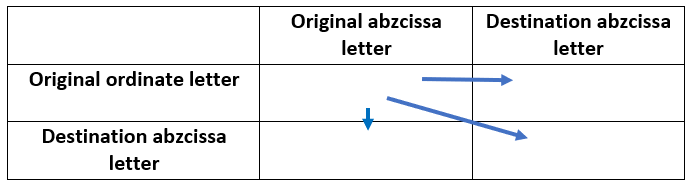
Finally, the path rules can be summarized into 4 scenarios:
| Scenario characteristic : | Scenario characteristic : | Result |
| Are the destination abscissa character and the destination ordinate character? | Type of arrow? | The operation applied to the current offset of the last version of the ordinate sequence |
| Same | ↘ | No modification |
| Different | → | After the origin ordinate offset, insertion of the offset from the abscissa destination offset |
| Different | ↘ | At the origin ordinate offset, substitution with the destination from the abscissa offset |
| Different | ↓ | Deletion of the origin ordinate offset |
The Levenshtein distance definition
Let’s define what has just been applied.
The distance between a sequence A and a sequence B is:
| In this case | Then the distance is | Explanation |
| If sequence A is empty | Then the distance is the length of sequence B | Because you remove successively all offsets of sequence B in order to transform it as empty |
| If sequence B is empty | Then the distance is the length of sequence A | Because you remove successively all offsets of sequence A in order to transform it as empty |
| If the last offset of B and the last offset of A are the same | Then the distance is the same as “A minus its last offset” with “B minus its last offset” | Because no transformation is needed |
| In all other cases | Then the distance is the minimum of these 3 distances: – “A minus its last offset” with “B” – “A” with “B minus its last offset” – “A minus its last offset” with “B minus its last offset” And then add 1 | Break down the problem and study these 3 scenarios; remove one character to the last offset of : – sequence A but not sequence B – sequence B but not sequence A – both sequences For each of the 3 scenarios, the simplification has reduced the distance by 1. Between the 3 scenarios, we choose the one with the minimum value, as the distance is defined by the shortest patch |
Indeed, a mathematical definition is described in Wikipedia:
The Levenshtein distance between two strings a,b (of length |a| and |b| respectively) is given by lev(a,b) where
where the tail of some string x is a string of all but the first character of x, and x[n] is the n nth character of the string x, starting with character 0.
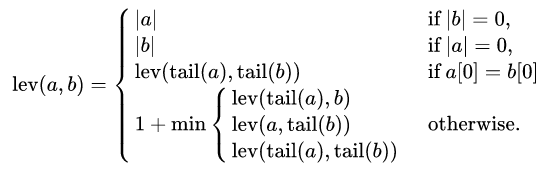
https://en.wikipedia.org/wiki/Levenshtein_distance#Definition
Remark:
- The easy definition is based on « head », meaning applying recursivity on the string minus the last character.
- The Wikipedia definition is based on « tail », meaning applying recursivity on the string minus the first character.
- Due to recursivity property, this is basically the same process.
Conclusion of the application of the algorithm
We were able to determine the distance between the strings LABO and LALAB. Also, we have explained how to convert step-by-step LABO to LALAB with the Levenshtein tools.
The next post will detail the calculation of Levenshtein distances with R programming between:
- LABO and LALAB, the example of this post
- And to determine from the examples, for each of the hereunder misspellings, between GOOGLE, APPLE, FACEBOOK, and AMAZON, which one is the most probable answer according to the Levenshtein distance:
- Gogglle
- Gougeule
- Googe
- Amazon
- Amzone
- Firstbok
- Alpes
- Aple
R Language programming example
We will apply R programming and recalculate this distance between LALO and LALAB. Moreover, we want to answer to the introduction: according to the Levenshtein metric, were the hereunder words meant to indicate GOOGLE, AMAZON, FACEBOOK, or APPLE?
- Gogglle
- Gougeule
- Googe
- Amazon
- Amzone
- Firstbok
- Alpes
- Aple
Choice of the R package for calculating the Levenshtein distance, and the first example
The classical algorithm which solves the Levenshtein distance is analytic: it means it will provide the exact solution. For example, the distance between LABO and LALAB is known and is exactly 3.
Indeed, according to some other data science algorithms, the Levenshtein one is not complex.
The function stringdist from the package stringdist is arbitrarily chosen, and will very soon be explained.
The hereunder example provides the Levenshtein distance between the word « LABO » and « LALAB ». Please note the function stringdist can calculate many types of distance, hence the parameter method = ‘lv’ is added
First, we need to declare our working environment
```{r}
# We call the package "stringdist" in order to calculate the Levenshtein distances
library(stringdist)
# A small test with the library
test_distance <- stringdist("LABO", "LALAB", method = "lv")
# Let's display the distance and check if it is 3 according to the previous post
test_distance
```
Solving the whole list with R programming
We are ready to solve the entire list:
- Gogglle
- Gougeule
- Googe
- Amazon
- Amzone
- Firstbok
- Alpes
- Aple
```{r}
# we declare data.table as usual
library(data.table)
#This vector is the list of words from the survey: the aim is to determine if
# they are closer to "Google", "Apple", "Facebook" or "Amazon"
# according to the Levenshtein distance
WORD <- c(
'Gogglle',
'Google',
'Gougeule',
'Googe',
'Amazon',
'Amzone',
'Firstbok',
'Alpes',
'Aple'
)
# We store the words in a data table
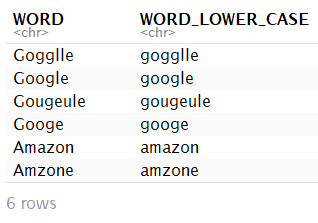
dt_survey <- data.table(WORD)
# Remember we have decided to be case-unsensitive
dt_survey <- dt_survey[ , WORD_LOWER_CASE := tolower(WORD) ]
head(dt_survey)
```
Now we calculate the distance of each word to each possible closer word « apple », « google », « amazon » and « facebook »
```{r}
# We keep dt_survey in a safe area, and create dt_survey2 as working area
dt_survey2 <- dt_survey
# Calculating the distance between the answer with Google company
dt_survey2 <- dt_survey2[, DIST_GOOGLE := stringdist(ANSWER, "google", method = "lv")]
# Calculating the distance between the answer with Apple company
dt_survey2 <- dt_survey2[, DIST_APPLE := stringdist(ANSWER, "apple", method = "lv")]
# Calculating the distance between the answer with Google company
dt_survey2 <- dt_survey2[, DIST_FACEBOOK := stringdist(ANSWER, "facebook", method = "lv")]
# Calculating the distance between the answer with Apple company
dt_survey2 <- dt_survey2[, DIST_AMAZON := stringdist(ANSWER, "amazon", method = "lv")]
head(dt_survey2)
```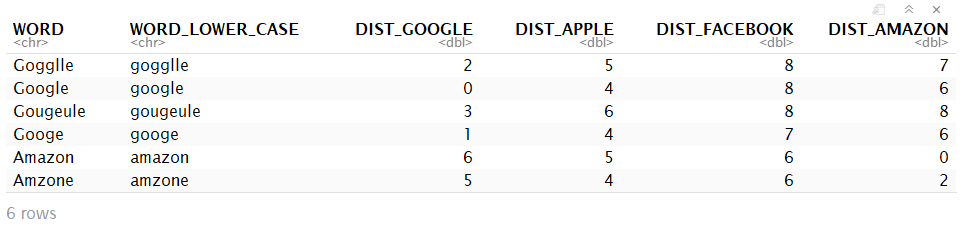
The Levenshtein distance between gogglle and google is 2
The Levenshtein distance between gogglle and apple is 5
The Levenshtein distance between gogglle and facebook is 8
The Levenshtein distance between gogglle and amazon is 7
The result in an intermediary data.table of the first rows
It is time for comparing the shortest distance for each word:
```{r}
# We keep dt_survey2 in a safe area, and create dt_survey3 as working area
dt_survey3 <- copy(dt_survey2)
# Find the minimum distance between the answer and the four company names
dt_survey3 <- dt_survey3[, MIN_DIST := pmin( DIST_GOOGLE, DIST_APPLE, DIST_FACEBOOK, DIST_AMAZON ) ]
# Populate the winner(s) for each possible scenario
dt_survey3 <- dt_survey3[, WINNER_GOOGLE := ifelse (DIST_GOOGLE == MIN_DIST, "google" ,"") ]
dt_survey3 <- dt_survey3[, WINNER_APPLE := ifelse (DIST_APPLE == MIN_DIST, "apple" ,"") ]
dt_survey3 <- dt_survey3[, WINNER_FACEBOOK := ifelse (DIST_FACEBOOK == MIN_DIST, "facebook" ,"") ]
dt_survey3 <- dt_survey3[, WINNER_AMAZON := ifelse (DIST_AMAZON == MIN_DIST, "amazon" ,"") ]
## Summarize the winner(s) in one single column
dt_survey3 <- dt_survey3[, CLOSEST_GAFA := paste(WINNER_GOOGLE, WINNER_APPLE, WINNER_FACEBOOK, WINNER_AMAZON, sep = " " )]
head(dt_survey3)
```
Explanation with the first row, which initial WORD is « gogglle »:
The distances, respectively with google, apple, facebook, and amazon are: 2, 5, 8, 7
Hence the minimum distance MIN_DIST is 2
This MIN_DIST is compared to the 4 distances: 2, 5, 8,7
If equal, it means it is the closest distance
For instance:
MIN_DIST is equal to DIST_GOOGLE: hence WINNER_GOOGLE is populated with « google »
MIN_DIST is not equal to DIST_APPLE: hence WINNER_APPLE is empty
MIN_DIST is not equal to DIST_FACEBOOK: hence WINNER_FACEBOOK is empty
MIN_DIST is not equal to DIST_AMAZON: hence WINNER_AMAZON is empty
CLOSEST_GAFA is filled with the concatenation of WINNER_GOOGLE, WINNER_FACEBOOK, WINNER_AMAZON, WINNER_AMAZON, with « space » as separator: the result is « google »
Note, a tie would be taken into account: CLOSEST_GAFA would contain the two or more winner thanks to the concatenation
As a summary, the picture represents the head of the data.table, and the last column CLOSEST_GAFA provides the winner or winners in case of a tie
As the data.table is crowded, we clean the result and display the entire data.table:
```{r}
# Let's display a clean result
dt_survey_final <- copy(dt_survey3)
dt_survey_final <- dt_survey_final[, c("WORD", "CLOSEST_GAFA")]
dt_survey_final
```
Conclusion of the R programming example
With R language, we have determined that « Gogglle » is closer to « Google » rather than « Amazon », « Facebook » or « Apple ».
The Levenshtein is a very simple distance for estimating the distance between two strings.
And as a corollary, it is useful for determining in a predefined list, which string is the closest to a reference string.
As the algorithm is easy to develop, you can find some Excel examples in order to calculate the Levenshtein distance:
This function example is interesting, as it provides the distance not absolute, but relative, as a percentage.